Resolução comentada do exercício 1.1.5 do livro do Tenembaum – Estruturas de Dados usando C.
O enunciado:
Conforme transcrição do exercício, é solicitado que se construa uma calculadora binária básica.
Escreva funções em C, add, subtract e multiply, que leiam duas strings de 0s e 1s representando inteiros não-negativos binários, e imprima a string representando a soma, a diferença e o produto, respectivamente.
Tenenbaum, Langsam e Augesnstein (2013)
Se você curtir esse artigo, dá uns cliques nos anúncios para ver o que o anunciante tem para te oferecer. Vou ficar muito contente.
Sabe o que é bacana dessa implementação?
Se você não gostar da solução que eu dei, basta apagar, mantendo os testes unitários. Daí, ao executar os testes unitários, vão subir os erros e aí é só você ir montando um código, chamando as funções, resolvendo os erros e implementando a solução no seu estilo. Tem jeito melhor de estudar?
E se…
Quando bati o olho nesse exercício, embora o caminho mais fácil seja ler as strings, as converter para decimal, fazer a conta e as converter de volta para binário e apresentar a saída, pensei na possibilidade de implementar um algoritmo capaz de representar o processo de soma e subtração binária, tal qual ensinado em livros como o do Tocci, Widmer e Moss (2015) pg 254, com direito ao cálculo de complemento de 1 e complemento de 2.
Segue um vídeo abaixo, como se calcula o complemento de 1 e de 2 para fazer uma subtração.
Adotando essa abordagem, significa que eu teria de manipular as strings de zeros e uns, fazer operações lógicas AND e OR, controlar o bit de overflow e implementar no código a lógica de Boole necessária para realizar essa soma, bit a bit, representada pelos caracteres “0” e “1”.
Como trabalhar com cada bit?
Para trabalhar com essa calculadora, eu tenho duas opções:
Uma opção seria pegar um byte (8 bits) e ir manipulando individualmente os seus bits, dado que a linguagem C tem ferramentas para fazer operações bit a bit.
A segunda opção, seria utilizar uma string de caracteres representando os bits zeros e uns da calculadora, evitando a manipulação direta bit a bit. O número zero e um seriam representados respectivamente pelos caracteres ‘0’ e ‘1’.
Embora a primeira opção seja mais hardcore e mais próxima à realidade, os bits zeros e uns teriam que ser obrigatoriamente convertidos para caracteres antes de serem impressos, aumentando a complexidade do programa e dificultando o entendimento das operações.
Então, por uma opção didática e para simplificar o processo de apresentação dos dados, optou-se pela escolha da segunda opção, ou seja, utilizar caracteres para representar os zeros e uns da calculadora ao invés de se trabalhar diretamente bit a bit.
Algumas decisões relativas ao programa:
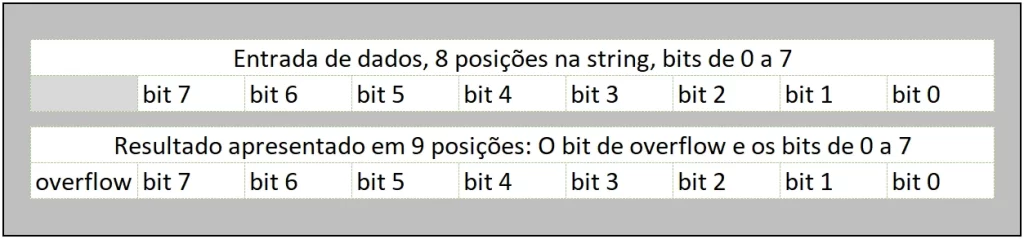
- Na entrada de dados, é possível inserir apenas 8 caracteres para representar cada um dos oito bits.
- Foram utilizados os caracteres ‘0’ (ASCII 48) e o ‘1’ (ASCII 49) para representar cada um dos possíveis bits.
- Internamente, esses 8 bits são concatenados em uma string com tamanho de 9 posições, sendo que a primeira posição serve para representar o sinal de sobrecarga (overflow) e as posições de 2 a 9 servem para acomodar os caracteres que representam cada um dos 8 bits a serem manipulados.
- Repetindo, internamente, o programa irá trabalhar com 1 caractere para gerenciar as operações matemáticas e 8 caracteres para acomodar o valor da conta, totalizando 9 caracteres que são numerados de bit 0 até bit 8, da direita para a esquerda.
- Como estamos utilizando 8 bits na entrada, é possível inserir os valores entre -128 até +127 e os resultados válidos das operações de soma, subtração e multiplicação devem estar entre -128 até +127, caso contrário o sistema deve indicar overflow.
- A posição 1 serve para representar o sinal de “vai um” ou overflow.
- O bit 7, sozinho, representa se o número é positivo “0” ou negativo “1”.
- Para gerenciamento de erros, os bits 8 e 7 representam juntos se o número é positivo “00” ou negativo “11”.
- Para gerenciamento de erros, os bits 8 e 7 representam juntos se ocorreu um erro de overflow, quando respectivamente assumem os valores “01” ou “10”, momento em que o resultado é inconsistente.
- As posições de 2 a 9 são reservadas para acomodar os bits 7, 6, 5, 4, 3, 2, 1 e 0 respectivamente. Conforme dito anteriormente, esses 8 bits podem representar valores entre -128 e +127.
- O bit zero, menos significativo, fica na posição 9 e o bit 7, mais significativo, fica na posição 2. Na posição 1 temos o bit 8 que é o sinal de overflow.
O código:
A montagem do código foi feita em 7 arquivos:
- main.c: Esse arquivo contém o main. Em loop contínuo, ele faz a entrada de dados e imprime o resultado da operação de soma, subtração e multiplicação, chamando as funções declaradas no arquivo calc.h.
- calc.h: Esse arquivo contém os protótipos das funções implementadas em calc.c.
- calc.c: Temos o arquivo calc.c contém a implementação das funções da calculadora binária.
- Testes_Calculadora.h: Contém os protótipos da funções implementadas em Testes_Calculadora.c.
- Testes_Calculadora.c: armazena os testes unitários que rodam utilizando a biblioteca CuTest.h / CuTest.c -> https://cutest.sourceforge.net/
Álgebra de Boole
Essa resolução adota a álgebra booleana para montar o circuito do somador virtual, que é o núcleo da montagem da calculadora de 8 bits.
Caso queira saber mais sobre o Logisim, no meu artigo “Arduino e Contador Hexa – parte 3“, eu abordei em detalhes como se faz para utilizar o Logisim como ferramenta de auxílio para aplicar a lógica digital na programação. Pode conferir esse artigo que é bem legal :-).
A tabela verdade:
Aqui no caso, eu vou mostrar a tabela verdade baseada no software Logisim, que utilizei para montar o circuito do somador bit a bit, mais a fórmula das saídas e o circuito digital equivalente, propriamente dito.
Essa tabela contém as regras do processo de soma entre dois bits. Ela cobre o funcionamento do sinal vai um.
O processamento dessa tabela, gera uma expressão lógica que pode ser utilizada para montar uma cláusula “if”, duas no caso, que servem para implementar a operação de soma.
Esse arquivo do Logisim está salvo no projeto, lá no GitHub, na pasta arquivos adicionais. Portanto você pode acessar diretamente, o abrir no Logisim e brincar com ele.
Abaixo tem a tabela verdade representando as opções possíveis no caso de soma de bits e o respectivo resultado esperado para a “saída” e para o valor “seta_vai_um”.
Note que estou simplesmente somando v1, com v2 e com vai um e na saída indico o resultado da soma e aviso quando é para mudar o estado de vai um de “1” para “0” e de “0” para “1”.
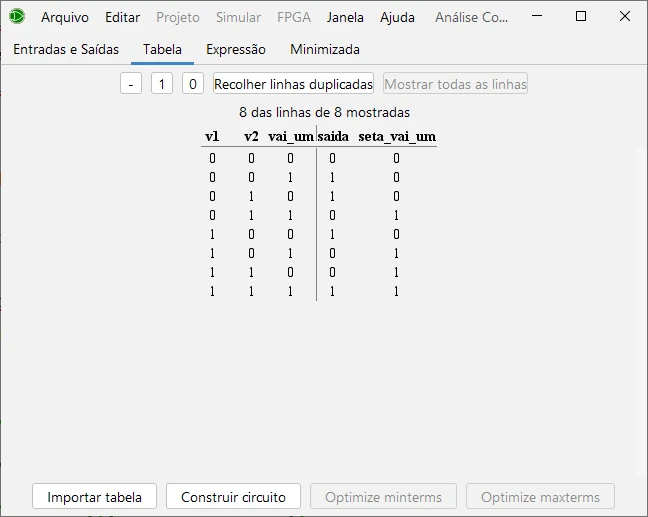
As fórmulas geradas pelo programa:
Uma vez carregada a tabela, manda-se construir o circuito e o Logisim Evolution faz as continhas para ti.
A função do circuito somador binário é fazer a soma dos bits “V1”, “V2” e “Vai um”, gerando os sinais “saída” e o “seta_vai_um”.
Aos Nerds de carteirinha, segue abaixo o print do mapa de Karnaugh com a respectiva fórmula gerada, transcrita abaixo.
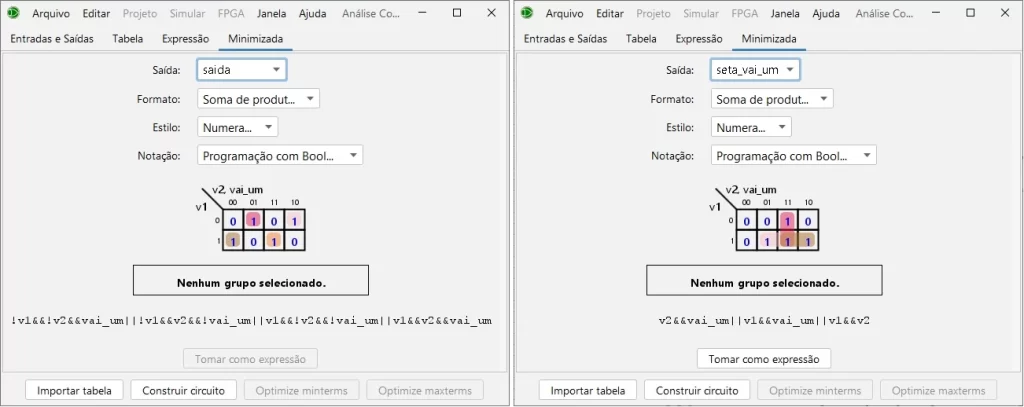
saida =~v1&~v2&vai_um|~v1&v2&~vai_um|v1&~v2&~vai_um|v1&v2&vai_um
seta_vai_um = v2&vai_um|v1&vai_um|v1&v2
Essa expressão lógica acima, no código, ela é representada dentro do bloco “for” conforme abaixo:
//Mandrakaria ativar! - Implementação do somador de oito bits com overflow:
for (controle = 9 ; controle >= 0; controle--){
soma_res[controle] = (invert(v1[controle])&invert(v2[controle])&vai_um)|
(invert(v1[controle])&v2[controle]&invert(vai_um))|
(v1[controle]&invert(v2[controle])&invert(vai_um))|
(v1[controle]&v2[controle]&vai_um);
if(((v2[controle]&vai_um)|
(v1[controle]&vai_um)|
(v1[controle]&v2[controle]))=='1'){
vai_um = '1';
}else{
vai_um = '0';
}
}
//Mandrakaria desativar!
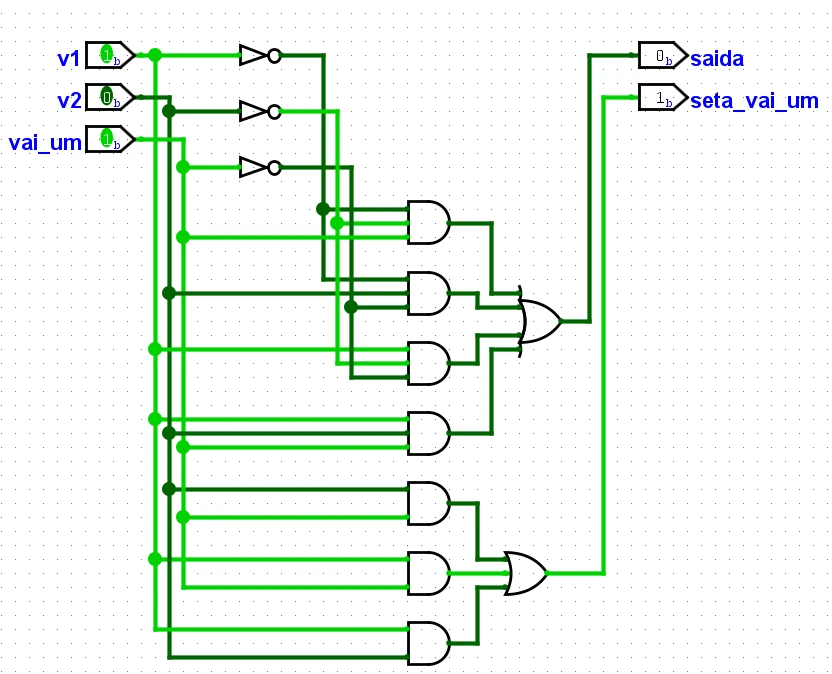
O circuito:
Abaixo temos o circuito equivalente que foi construído pelo Logisim Evolution, a partir dos dados inseridos na tabela. Se a gente comprar os componentes certos, dá para montar e fazer funcionar no hardware esse trecho de código da expressão lógica. É bem legal isso aí :-).
E o código?
Aqui tem o código para te dar uma base, mas se quiser baixar e compilar, recomendo que você pegue a versão mais atualizada dele, que está disponível no meu repositório do GitHub.
Segue o main.c
A linha 43 tem uma flag para disparar a suite de testes.
- DEBUG==1, executa os testes unitários
- DEBUG==0, entra em operação normal
O main() é bem simples. Apenas chama as funções de soma, subtração e multiplicação e faz a impressão dos resultados.
Lá na linha 88 tem a chamada “RunAllTests()” que executa os testes unitários.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <windows.h>
#include "calc.h"
#include "Teste_unitario/CuTest.h"
#include "Teste_unitario/Testes_Calculadora.h"
#define DEBUG 0
/*
Tenenbaum 1.1.5
Escreva funcoes em C, add, subtract e multiply, que leiam duas strings
de Os e ls representando inteiros nao-negativos binarios, e imprima a
string representando a soma, a diferenca e o produto, respectivamente.
Este codigo implementa controle de erro de soma e subtracao de numeros
positivos e negativos, como um opcional.
Este codigo apresenta resultados validos cujo resultados estejam entre
os valores de -127 a +128.
Este código comentado esta no site https://nets-nuts.com.br.
No caminho Notas de aulas -> Estruturas de dados usando C.
Autor: Renato de Pierri.
*/
//Suite de testes
CuSuite* CuGetSuite();
CuSuite* CuStringGetSuite();
//Suite de testes
int main(){
int le_dado();
int le_dado(char word[]);
int eerro;
int erro_1=1, erro_2=1;
static char valor_1[9],
valor_2[9],
soma_resultado[10],
sub_resultado[10],
mult_resultado[10];
// DEBUG == 1: Debug | DEBUG == 0: Operacao normal
if (DEBUG == 0){
while(1){
while(erro_1 == 1||erro_2 == 1){
printf("digite o primeiro valor binario de ate 8 bits\n");
erro_1 = le_dado(valor_1);
printf("digite o segundo valor binario de ate 8 bits\n");
erro_2 = le_dado(valor_2);
if(erro_1 == 1 || erro_2==1){
printf("valor invalido, digite novamente todos os valores\n") ;
Sleep(3000);
system("cls");
erro_1 = 1;
erro_2 = 1;
}
}
printf("Resultados validos entre -128 ate +127 - 10000000 ate 01111111\n\n");
strcpy(soma_resultado,soma(valor_1, valor_2));
printf ("Operacao de soma\n");
printf("Resultado = %s\n",
&(soma_resultado[strlen (soma_resultado)-8]));
eerro = verifica_erro(soma_resultado);
printf("Erro de soma ----------: %d\n\n",eerro);
strcpy (sub_resultado, subtrai(valor_1, valor_2));
printf("Operacao de subtracao\n");
printf ("Resultado = %s\n",
&(sub_resultado[strlen (sub_resultado) - 8]));
eerro = verifica_erro(sub_resultado);
printf("Erro de subtracao -----: %d\n\n",eerro);
strcpy(mult_resultado, multiplica(valor_1, valor_2));
printf("Operacao de multiplicacao\n");
printf ("Multiplicacao = %s\n",
&(mult_resultado[strlen (mult_resultado)-8]));
eerro = verifica_erro(mult_resultado);
printf("Erro de multiplicacao nao foi implementado.\n"
"Apresenta resultados validos somente entre -128 e +127\n\n");
system("pause");
system("cls");
erro_1=1;
}
}else{
RunAllTests();
}
return 0;
}
segue o calc.h:
Aqui tem as declarações das funções:
- le_dado: Faz a leitura dos dados de entrada.
- alinha_direita: alinha a string à direita e preenche com zeros até concluir 8 bits.
- soma: Faz a operação de soma.
- compl_1: Calcula o complemento de 1.
- compl_2: Calcula o complemento de 2.
- subtrai: Faz a operação de subtração..
- multiplica: Faz a operação de multiplicação.
- invert: Manda um caractere “0” e ele volta “1” e vice versa.
- verifica_erro: Verifica a operação deu erro.
- completa: Completa a string à direita com um ou zero, conforme o caso.
- encurta: Reduz o tamanho da string de 9 para 8 bits.
- verifica_sinal: Aplica a regra matemática do sinal na multiplicação.
#ifndef CALC_H_INCLUDED
#define CALC_H_INCLUDED
int le_dado(char word[]);
void alinha_direita(char word[]);
char* soma(char valor_1[], char valor_2[]);
const char * compl_1(char v2[]);
const char * compl_2(char comp_1[]);
char * subtrai(char valor_1[], char valor_2[]);
char * multiplica(char valor_1[], char valor_2[]);
char invert(char bit);
int verifica_erro(char res[]);
void completa(char saida[],char entrada[] );
void encurta(char word[]);
int verifica_sinal(char fator1, char fator2);
#endif // CALC_H_INCLUDED
Segue o calc.c:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <windows.h>
#include "calc.h"
#define NEGATIVO 1
int le_dado(char word[]){
int controle, check, tamanho_string;
check = 0;
controle = 0;
scanf("%8s",word);
fflush(stdin);
//Verifica se tem apenas "um" e "zeros"
tamanho_string = strlen(word);
while (controle < tamanho_string){
if (word[controle]== '0'||word[controle] == '1'){
check = 0;
controle++;
}else{
check = 1;
controle = tamanho_string;
}
}
alinha_direita(word);
printf("string completa: %s\n", word);
return check;
}
//void soma(char valor_1[], char valor_2[], char soma_res[]){
char* soma(char valor_1[], char valor_2[]){
int controle = 0;
static char v1[9],v2[9];
static char vai_um = '0';
static char soma_res[10];
int tamanho = strlen (valor_1);
if (tamanho == 8){
completa(v1, valor_1);
completa(v2, valor_2);
}else{
strcpy(v1,valor_1);
strcpy(v2,valor_2);
}
strcpy(soma_res,"ABCDEFGHI");
vai_um = '0';
//Mandrakaria ativar! - Implementação do somador de oito bits com overflow:
for (controle = 9 ; controle >= 0; controle--){
soma_res[controle] = (invert(v1[controle])&invert(v2[controle])&vai_um)|
(invert(v1[controle])&v2[controle]&invert(vai_um))|
(v1[controle]&invert(v2[controle])&invert(vai_um))|
(v1[controle]&v2[controle]&vai_um);
if(((v2[controle]&vai_um)|
(v1[controle]&vai_um)|
(v1[controle]&v2[controle]))=='1'){
vai_um = '1';
}else{
vai_um = '0';
}
}
//Mandrakaria desativar!
soma_res[9]='\0';
return soma_res;
}
const char * compl_1(char v2[]){
int varre;
static char comp_1[9];
for(varre = 8; varre >=0; varre--){
comp_1[varre] = invert(v2[varre]);
}
return comp_1;
}
const char * compl_2(char comp_1[]){
static char comp_2[9];
strcpy(comp_2,soma("000000001",comp_1));
return comp_2;
}
char * subtrai(char valor_1[], char valor_2[]){
static char v1[9],v2[9];
static char complemento_1[9], complemento_2[9];
static char sub_res[9];
completa(v1, valor_1);
completa(v2, valor_2);
sub_res[0]='0';
strcpy (complemento_1, compl_1(v2));
strcpy (complemento_2, compl_2(complemento_1));
strcpy (sub_res, soma(v1,complemento_2));
return sub_res;
}
char * multiplica(char valor_1[], char valor_2[]){
static char fator1[9],fator2[9],ct[9], temp[9];
static char mult_res[10];
static char complemento_1[9];
int sinal;
strcpy (fator1, valor_1);
strcpy (fator2, valor_2);
strcpy (ct, valor_2);
// char sinal = v2[0];
strcpy(mult_res,"000000000");
strcpy(temp,"00000000");
if(ct[0] == '1'){
while((ct[0]|ct[1]|ct[2]|ct[3]|ct[4]|ct[5]|ct[6]|ct[7])!='0'){
strcpy(temp,(soma(temp,fator1))+1);
strcpy(ct,((soma(ct,"00000001"))+1));
}
}else{
while((ct[0]|ct[1]|ct[2]|ct[3]|ct[4]|ct[5]|ct[6]|ct[7]|ct[8])!='0'){
strcpy(temp,(soma(temp,fator1))+1);
strcpy(ct,((subtrai(ct,"00000001"))+1));
}
}
sinal = verifica_sinal(fator1[0], fator2[0]);
if((sinal == NEGATIVO)||(temp[0]=='1')){
char f1 = invert(fator1[0]);
char f2 = fator2[0];
if((f1=='1')&(f2=='1')||(f1=='0')&(f2=='1')){
strcpy (complemento_1, compl_1(temp));
complemento_1[8]='\0';
completa(temp,complemento_1);
strcpy (mult_res, compl_2(temp));
}else{
completa(mult_res,temp);
}
}else{
completa(mult_res,temp);
}
return mult_res;
}
char invert(char bit){
if (bit == '0'){
bit = '1';
}else{
bit = '0';
}
return bit;
}
//controle de erro. Precisa implementar
int verifica_erro(char res[]){
int erro = 1;
char res_0 = res[0];
char res_1 = res[1];
char i_res_0 = invert(res[0]);
char i_res_1 = invert(res[1]);
if(((i_res_0&res_1)|(res_0&i_res_1))=='1'){
erro = 1;
}else{
erro=0;
}
return erro;
}
int verifica_sinal(char fator1, char fator2){
int erro = 1;
char i_fator1 = invert(fator1);
char i_fator2 = invert(fator2);
if(((i_fator1&fator2)|(fator1&i_fator2))=='1'){
erro = 1;
}else{
erro=0;
}
return erro;
}
void completa(char saida[],char entrada[] ){
if (entrada[0] == '1'){
saida[0] = '1';
}else{
saida[0]='0';
}
int controle = 1;
while (controle <= 9){
saida[controle] = entrada[controle-1];
controle++;
}
// saida[9]='\0';
return;
}
void encurta(char word[]){
int tamanho_string = 8;
int varre;
//Alinhando a direita
tamanho_string--;
for(varre = 10; varre >=0; varre--){
if(tamanho_string >= 0){
word[varre] = word[tamanho_string];
tamanho_string --;
}else{
word[varre] = '0';
}
}
word[9]='\0';
if (word[1]=='1'){word[0]='1';}
return;
}
void alinha_direita(char word[]){
int tamanho_string, varre;
tamanho_string = strlen(word);
if(tamanho_string < 8){
tamanho_string--;
for(varre = 7; varre >=0; varre--){
if(tamanho_string >= 0){
word[varre] = word[tamanho_string];
tamanho_string --;
}else{
word[varre] = '0';
}
}
}
return;
}
O que pode ser melhorado:
Tratamento de overflow:
Precisaria implementar o controle de overflow na multiplicação. Há várias maneiras de proceder. Deixo para desenvolver futuramente.
Algumas considerações:
Abaixo seguem as condições de overflow que foram mapeadas.
- 127 positivo em binário significa 01111111.
- 128 negativo significa 10000000 em binário
- Se eu somar 1 positivo ao valor 127 positivo, o resultado seria 128 positivo ou 10000000. Só que esse número binário é reservado para representar o valor 128 negativo, portanto é uma condição de erro.
- O mesmo vale se eu somar negativo 1 a negativo 128. Daria negativo 129 que é mais que negativo 128. Isso também é um erro e o programa deve indicar.
- Caso uma operação de soma ou subtração caia nessa condição, é um estado de erro e o programa deve indicar erro
- O tratamento de erro pode ser facilmente implementado, fazendo uma operação de exclusive OR entre o bit 8 e o bit 9 do resultado. Conforme informado, quando esses dois bits são diferentes, a condição de erro está ativa :-).
- A tabela abaixo detalha algumas operações e o resultado esperado, utilizadas no teste unitário:
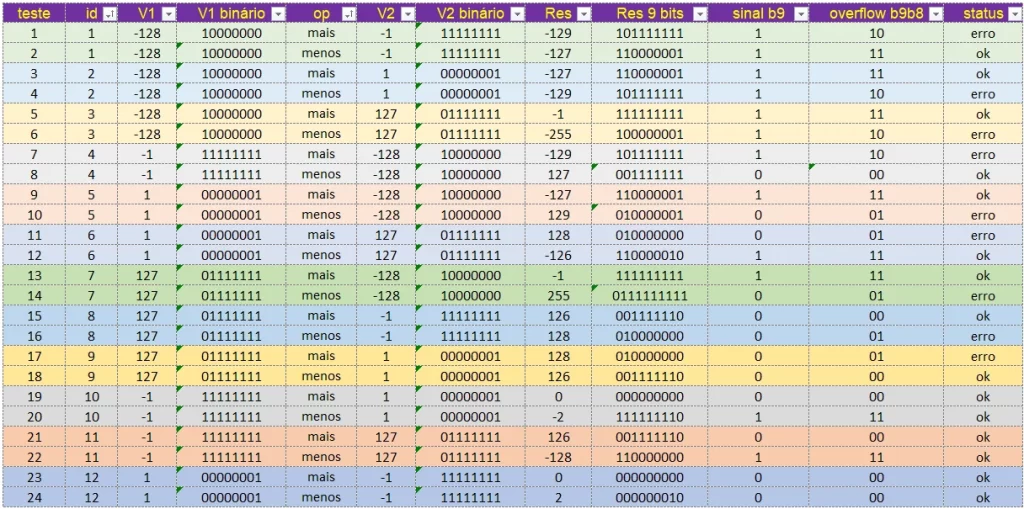
Esse código está disponível para download no Github, clicando aqui.
Testes unitários:
Abaixo segue o arquivo Testes_Calculadora.c com os testes unitários, documentando o funcionamento da calculadora:
#include <stdio.h>
#include <stdlib.h>
#include "../calc.h"
#include "CuTest.h"
CuSuite* StrUtilGetSuite();
void TesteNato(char oi[]);
void RunAllTests(void){
CuString* output = CuStringNew();
CuSuite* suite = CuSuiteNew();
CuSuiteAddSuite(suite, StrUtilGetSuite());
CuSuiteRun(suite);
CuSuiteSummary(suite, output);
CuSuiteDetails(suite, output);
printf ("%s\n\n", output->buffer);
}
// Testes unitarios
//Testes de soma
void TesteSoma1(CuTest *tc){
char * input1 = "10000000";
char * input2 = "11111111";
char * actual = soma(input1, input2);
char * expected = "101111111";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSoma2(CuTest *tc){
char * input1 = "10000000";
char * input2 = "00000001";
char * actual = soma(input1, input2);
char * expected = "110000001";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSoma3(CuTest *tc){
char * input1 = "10000000";
char * input2 = "01111111";
char * actual = soma(input1, input2);
char * expected = "111111111";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSoma4(CuTest *tc){
char * input1 = "11111111";
char * input2 = "10000000";
char * actual = soma(input1, input2);
char * expected = "101111111";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSoma5(CuTest *tc){
char * input1 = "00000001";
char * input2 = "10000000";
char * actual = soma(input1, input2);
char * expected = "110000001";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSoma6(CuTest *tc){
char * input1 = "00000001";
char * input2 = "01111111";
char * actual = soma(input1, input2);
char * expected = "010000000";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSoma7(CuTest *tc){
char * input1 = "01111111";
char * input2 = "10000000";
char * actual = soma(input1, input2);
char * expected = "111111111";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSoma8(CuTest *tc){
char * input1 = "01111111";
char * input2 = "11111111";
char * actual = soma(input1, input2);
char * expected = "001111110";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSoma9(CuTest *tc){
char * input1 = "01111111";
char * input2 = "00000001";
char * actual = soma(input1, input2);
char * expected = "010000000";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSoma10(CuTest *tc){
char * input1 = "11111111";
char * input2 = "00000001";
char * actual = soma(input1, input2);
char * expected = "000000000";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSoma11(CuTest *tc){
char * input1 = "11111111";
char * input2 = "01111111";
char * actual = soma(input1, input2);
char * expected = "001111110";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSoma12(CuTest *tc){
char * input1 = "00000001";
char * input2 = "11111111";
char * actual = soma(input1, input2);
char * expected = "000000000";
CuAssertStrEquals (tc, expected, actual);
}
//Testes de subtracao
void TesteSub1(CuTest *tc){
char * input1 = "10000000";
char * input2 = "11111111";
char * actual = subtrai(input1, input2);
char * expected = "110000001";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSub2(CuTest *tc){
char * input1 = "10000000";
char * input2 = "00000001";
char * actual = subtrai(input1, input2);
char * expected = "101111111";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSub3(CuTest *tc){
char * input1 = "10000000";
char * input2 = "01111111";
char * actual = subtrai(input1, input2);
char * expected = "100000001";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSub4(CuTest *tc){
char * input1 = "11111111";
char * input2 = "10000000";
char * actual = subtrai(input1, input2);
char * expected = "001111111";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSub5(CuTest *tc){
char * input1 = "00000001";
char * input2 = "10000000";
char * actual = subtrai(input1, input2);
char * expected = "010000001";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSub6(CuTest *tc){
char * input1 = "00000001";
char * input2 = "01111111";
char * actual = subtrai(input1, input2);
char * expected = "110000010";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSub7(CuTest *tc){
char * input1 = "01111111";
char * input2 = "10000000";
char * actual = subtrai(input1, input2);
char * expected = "011111111";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSub8(CuTest *tc){
char * input1 = "01111111";
char * input2 = "11111111";
char * actual = subtrai(input1, input2);
char * expected = "010000000";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSub9(CuTest *tc){
char * input1 = "01111111";
char * input2 = "00000001";
char * actual = subtrai(input1, input2);
char * expected = "001111110";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSub10(CuTest *tc){
char * input1 = "11111111";
char * input2 = "00000001";
char * actual = subtrai(input1, input2);
char * expected = "111111110";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSub11(CuTest *tc){
char * input1 = "11111111";
char * input2 = "01111111";
char * actual = subtrai(input1, input2);
char * expected = "110000000";
CuAssertStrEquals (tc, expected, actual);
}
void TesteSub12(CuTest *tc){
char * input1 = "00000001";
char * input2 = "11111111";
char * actual = subtrai(input1, input2);
char * expected = "000000010";
CuAssertStrEquals (tc, expected, actual);
}
//Complemento de 1 e complemento de 2
void Complemento_1(CuTest *tc){
char * input1 = "111100001";
char * actual = compl_1(input1);
char * expected = "000011110";
CuAssertStrEquals (tc, expected, actual);
}
void Complemento_2_128n(CuTest *tc){
char * input1 = "001111111";
char * actual = compl_2(input1);
char * expected = "010000000";
CuAssertStrEquals (tc, expected, actual);
}
void Complemento_2_1n(CuTest *tc){
char * input1 = "000000000";
char * actual = compl_2(input1);
char * expected = "000000001";
CuAssertStrEquals (tc, expected, actual);
}
void Complemento_2_1p(CuTest *tc){
char * input1 = "111111110";
char * actual = compl_2(input1);
char * expected = "111111111";
CuAssertStrEquals (tc, expected, actual);
}
void Complemento_2_127p(CuTest *tc){
char * input1 = "110000000";
char * actual = compl_2(input1);
char * expected = "110000001";
CuAssertStrEquals (tc, expected, actual);
}
void TestMult1(CuTest *tc){
char * input1 = "00000011";
char * input2 = "00000100";
char * actual = multiplica(input1, input2);
char * expected = "000001100";
CuAssertStrEquals (tc, expected, actual);
}
void mais3__x__mais2(CuTest *tc){
char * input1 = "00000011";
char * input2 = "00000010";
char * actual = multiplica(input1, input2);
char * expected = "000000110";
CuAssertStrEquals (tc, expected, actual);
}
void mais3__x_menos2(CuTest *tc){
char * input1 = "00000011";
char * input2 = "11111110";
char * actual = multiplica(input1, input2);
char * expected = "111111010";
CuAssertStrEquals (tc, expected, actual);
}
void menos3_x__mais2(CuTest *tc){
char * input1 = "11111101";
char * input2 = "00000010";
char * actual = multiplica(input1, input2);
char * expected = "111111010";
CuAssertStrEquals (tc, expected, actual);
}
void menos3_x_menos2(CuTest *tc){
char * input1 = "11111101";
char * input2 = "11111110";
char * actual = multiplica(input1, input2);
char * expected = "000000110";
CuAssertStrEquals (tc, expected, actual);
}
CuSuite*StrUtilGetSuite(){
CuSuite* suite = CuSuiteNew();
SUITE_ADD_TEST(suite,TesteSoma1);
SUITE_ADD_TEST(suite,TesteSoma2);
SUITE_ADD_TEST(suite,TesteSoma3);
SUITE_ADD_TEST(suite,TesteSoma4);
SUITE_ADD_TEST(suite,TesteSoma5);
SUITE_ADD_TEST(suite,TesteSoma6);
SUITE_ADD_TEST(suite,TesteSoma7);
SUITE_ADD_TEST(suite,TesteSoma8);
SUITE_ADD_TEST(suite,TesteSoma9);
SUITE_ADD_TEST(suite,TesteSoma10);
SUITE_ADD_TEST(suite,TesteSoma11);
SUITE_ADD_TEST(suite,TesteSoma12);
SUITE_ADD_TEST(suite,Complemento_1);
SUITE_ADD_TEST(suite,Complemento_2_128n);
SUITE_ADD_TEST(suite,Complemento_2_1n);
SUITE_ADD_TEST(suite,Complemento_2_1p);
SUITE_ADD_TEST(suite,Complemento_2_127p);
SUITE_ADD_TEST(suite,TesteSub1);
SUITE_ADD_TEST(suite,TesteSub2);
SUITE_ADD_TEST(suite,TesteSub3);
SUITE_ADD_TEST(suite,TesteSub4);
SUITE_ADD_TEST(suite,TesteSub5);
SUITE_ADD_TEST(suite,TesteSub6);
SUITE_ADD_TEST(suite,TesteSub7);
SUITE_ADD_TEST(suite,TesteSub8);
SUITE_ADD_TEST(suite,TesteSub9);
SUITE_ADD_TEST(suite,TesteSub10);
SUITE_ADD_TEST(suite,TesteSub11);
SUITE_ADD_TEST(suite,TesteSub12);
SUITE_ADD_TEST(suite,TestMult1);
SUITE_ADD_TEST(suite,mais3__x__mais2);
SUITE_ADD_TEST(suite,mais3__x_menos2);
SUITE_ADD_TEST(suite,menos3_x__mais2);
SUITE_ADD_TEST(suite,menos3_x_menos2);
return suite;
}
Está aí a resolução. Pode-se dizer que fiz mais que o solicitado, mas é o seguinte. Se limitarmos a entrada para somente números de 7 bits, positivos, entendo que estaremos cumprindo os requisitos do exercício, ainda mais que o exercício não especificou quantos bits deveria ter a calculadora.
Programas utilizados:
Para programar em C, pode ser qualquer IDE de sua preferência. No meu caso, utilizei o CodeBlocks com o compilador GCC.
Para ajudar na resolução, foi utilizado o programa Logisim Evolution que pode ser baixado diretamente no site do Source Forge, lembrando que ele precisa do OpenJDK instalado, que pode ser baixado direto do site da Microsoft.
Para o pessoal do Linux, basta pesquisar como faz para instalar ambos, de acordo com sua distro. Garanto que é mais fácil que no Windows.
Esses softwares também podem ser instalados a partir do gerenciador de software Chocolatey, que é uma mão na roda.
Aprendendo muito:
Meu jovem, encare isso como alguém fazendo um quebra cabeça nas horas vagas enquanto dá uma estudadinha nos algoritmos. Entre em contato. Vou gostar de conversar sobre isso.
Abraços.
Bibliografia:
TENENBAUM, Aaron M.; LANGSAM, Yedidyah; AUGESNSTEIN, Moshe J.. Estruturas de Dados Usando C. São Paulo: Pearson, 2013. 884 p. ISBN 13: 978-85-346-0348-5
TOCCI, Ronald J.; WIDMER, Neal S.; MOSS, Gregory L.. Sistemas Digitais: princípios e aplicações. 11. ed. São Paulo: Pearson, 2015. 819 p. ISBN: 978-85-7605-922-6.
Postado em 30/12/2012 por Renato de Pierri