Resposta publicada no Quora em 19/04/2021
Em computação, hexadecimal é muito mais fácil de entender.
Quando um programador que manja de hardware olha para um código hexadecimal, ele sabe exatamente como o hardware está se comportando, apenas fazendo contas de cabeça.
Por isso que o hexadecimal é utilizado.
Não leia o resto.
Modo nerdice on.
Computador trabalha com lógica binária.
Pensando em um computador de 8 bits, sabemos que ele consegue manusear 8 bits por vez em sua linha de dados.
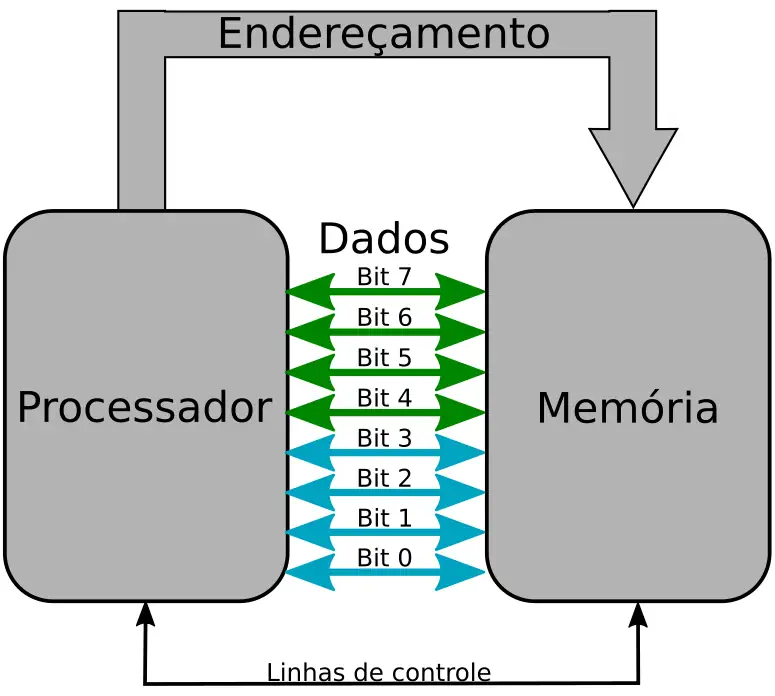
No diagrama abaixo temos um computador simplificado:
- Do lado esquerdo tem o processador e do lado direito tem a memória. Deixei de fora alguns detalhes para ficar mais fácil a explicação.
- O processador e a memória são interligados pelo barramento de endereçamento, de dados e as linhas de controle.
- O barramento de dados está detalhando os 8 bits que o compõe.
- Cada seta no barramento de dados representa um bit de dados.
- O processador consegue ler e escrever na memória, 8 bits de dados por vez, pois trata-se de um computador de 8 bits.
Os bits, são essas linhas que podem assumir valores binários de zero ou um.
Eletronicamente falando:
Essas linhas dos bits de dados podem estar energizadas ou não.
As linhas que estiverem energizadas terão o valor lógico VERDADEIRO (1 – um) e as que não estiverem energizadas terão o valor lógico FALSO (0 – zero).
Onde entra o hexadecimal:
Note que o barramento de dados foi separado em dois conjuntos de 4 bits.
- Um conjunto de 4 bits engloba os bits de 0 a 3
- O segundo conjunto de 4 bits engloba os bits de 4 a 7
A pergunta que a gente faz agora é: Quantas combinações a gente consegue fazer de bits ligados e desligados aqui?
Já dou a resposta, que são 256 combinações indo de todos os 8 bits com valor FALSO – desligados até termos todos os 8 bits com o valor VERDADEIRO – ligados.
Acompanhe, analisando os 4 primeiros bits:
Os caras fizeram o seguinte, os quatro primeiros bits, dá para fazer 16 combinações indo do valor decimal zero até o valor decimal 15. Basta continuar com a tabela adicionando os bits que faltam e iremos chegar em 256 combinações, podendo representar os números de zero a 255..
Mais um detalhe: A posição do bit corresponde a um valor decimal. Se os bits zero e dois forem verdadeiros, significa que temos o número 5 nas notações decimal e hexadecimal, por exemplo.
Conforme dito, se pegar o segundo conjunto de 4 bits, também dá para fazer essas dezesseis combinações.
Juntando o primeiro e o segundo conjunto de 4 bits, dá para fazer 16 X 16 combinações, ou seja, dá para fazer 256 combinações, que é capaz de representar os valores decimais indo de zero a 255.
No fim de tudo é isso o que realmente importa:
Para simplificar isso aí, os bits são separados em grupos de 4 bits que são representados pelos símbolos indo de “0” até “F”.
Um código indicando quais linhas de cada conjunto de 4 bits estão ligadas ou desligadas.
Simples e brilhante.
Desenvolvendo computadores:
Agora, se coloque no lugar do desenvolvedor de computadores.
O cara tem que lidar com o circuito elétrico. Tem que olhar para um código e decodificar de cabeça quais linhas do barramento de dados estão energizadas ou não.
É muito mais fácil para um engenheiro de hardware:
- Separar a linha de dados em grupos de 4 bits.
- Trabalhar com a notação hexadecimal, 3A por exemplo.
- Converter esse número, de cabeça para o binário “0011 1010”.
- E identificar no barramento quais linhas de dados que estão energizadas ou não…
Do que fazer a conversão do número 58 (decimal) para seu correspondente binário, que é bem mais complicado.
É por isso que se utiliza o hexadecimal.
Hexadecimal é para humanos falarem com máquinas, enquanto que decimal é para máquinas falarem com humanos.
Recomendo que seja lido o livro do Tocci, que já indiquei em outras respostas por aqui.
Fontes:
Livro do Tocci:https://loja.grupoa.com.br/sistemas-digitais-principios-e-aplicacoes-12ed9788543025018-p1005546?tsid=34
Demais tabelas e infográficos: Acervo pessoal.